ESTATÍSTICA - DESCRIÇÃO DE DADOS - MÉDIA GEOMÉTRICA
CONHECIMENTOS BANCÁRIOS
MATEMÁTICA
NOÇÕES DE ESTATÍSTICA
2.2. MÉDIA GEOMÉTRICA (Revisada em 07-03-2024)
Coletânea por Américo G Parada Fº - Contador - Coordenador do COSIFE - ex Auditor do BACEN
Publicado por BRASIL ESCOLA / UOL. Autor: OLIVEIRA, Raul Rodrigues de. "Média geométrica" (Acessado em 16/08/2021)
2.2.1. DEFINIÇÕES
A média geométrica junto à média aritmética e à média harmônica foram desenvolvidas pela escola pitagórica. Na estatística é bastante comum a busca pela representação de um conjunto de dados por um único valor para tomada de decisões. Uma das possibilidades para o valor central é a média geométrica.
Ela é útil para representação de um conjunto que possui dados que se comportam próximo a uma progressão geométrica, também para encontrar o lado de quadrado e cubo, conhecendo a área e o volume respectivamente. A média geométrica é aplicada também em situações de acumulação de aumento ou decrescimento percentual. Para calcular a média geométrica de um conjunto de n valores, calculamos a raiz enésima do produto dos elementos, ou seja, se um conjunto possui três termos, por exemplo, multiplicamos os três e calculamos a raiz cúbica do produto.
A análise estatística é essencial para a tomada de decisões, por exemplo, a seleção do melhor tipo de média para representar um conjunto.
Segundo o contador (auditor) Américo G Parada Fº, o estudo da Média Geométrica também possibilita o aprendizado da aplicação de vários segmentos da Matemática como a FATORAÇÃO e uma série de números com o intuito de ser obtida a RAIZ (quadrada, cúbica...).
2.2.2. FORMULA DA MÉDIA GEOGRÁFICA
A média geométrica é utilizada para encontrar um valor médio entre um conjunto de dados. Para calcular-se a média geométrica, é necessário um conjunto com dois ou mais elementos. Seja A um conjunto de dados A = (x1, x2, x3, ... xn), um conjunto com n elementos, a média geométrica desse conjunto é calculada por:
![]()
Leia também: Medidas de dispersão: amplitude e desvio
2.2.3. CÁLCULO DA MÉDIA GEOMÉTRICA
Seja A = {3,12,16,36}, qual será a média geométrica desse conjunto?
Resolução:
Para calcularmos a média geométrica, primeiro contamos a quantidade de termos do conjunto, no caso n = 4. Então temos que:
MÉTODO 1: REALIZANDO AS MULTIPLICAÇÕES
![]()
NOTA DO COSIFE:
No caso em questão, as raízes biquadradas e o multiplicador poderiam ser representados na forma exponencial pelas seguintes expressões algébricas (por Américo G Parada Fº - Contador):
x = y1/n :: n = 4 :: x = y1/4
x = (3 * 12 * 16 * 36)1/4
x = (20735)1/4
x = 12
OBSERVAÇÕES: * = multiplicado = multiplicador
Expoente 1/n = raiz n :: Expoente 1/2 = 0,5 = Raiz Quadrada :: Expoente 1/3 = 0,333... = raiz cúbica :: Expoente 1/4 = 0,25 = raiz biquadrada
Como nem sempre temos à disposição a calculadora para realização das multiplicações, é possível fazer o cálculo com base na fatoração de um número natural.
MÉTODO 2: FATORAÇÃO

Utilizando as fatorações temos que:
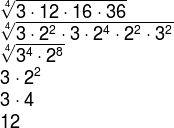
NOTA DO COSIFE:
No caso em questão, as raízes biquadradas poderiam ser representadas na forma exponencial pelas seguintes expressões algébricas (por Américo G Parada Fº - Contador):
x = y1/n :: n = 4 :: x = y1/4
x = (3 * 12 * 16 * 36)1/4
x = [3 * (22 * 3) * 24 * (22 * 32)]1/4
x = (34 * 28)1/4 = (3 * 22)
x = (3 * 4)
x = 12
Observação: * = multiplicado = multiplicador :: y1/4 = y0,25 = Raiz biquadrada de y
Aplicações da média geométrica
A média geométrica pode ser aplicada em qualquer conjunto de dados estatístico, mas normalmente ela é empregada na geometria, para comparar lados de prismas e cubos de mesmo volume, ou quadrados e retângulos de mesma área. Há também aplicação em problemas da matemática financeira que envolvam taxa percentual acumulada, ou seja, porcentagem sob porcentagem. Além de ser a média mais conveniente para dados que se comportam como uma progressão geométrica.
Exemplo 1: Aplicação em porcentagem.
Um produto, durante três meses, teve aumentos consecutivos, o primeiro foi de 20%, o segundo de 10% e o terceiro de 25%. Qual foi o aumento médio percentual ao final desse período?
Resolução
O produto custava inicialmente 100%, logo no primeiro mês ele passou a custar 120%, que, na sua forma decimal, escreve-se 1,2. Esse raciocínio será o mesmo para os três aumentos, então queremos a média geométrica entre: 1,2; 1,1; e 1,25.
![]()
O aumento é de 18,2% por mês em média.
NOTA DO COSIFE:
No caso em questão, as raízes cúbicas poderiam ser representadas na forma exponencial pelas seguintes expressões algébricas (por Américo G Parada Fº - Contador):
x = y1/n :: n = 3 :: x = y1/3
x = (1,2 * 1,1 * 1,25)1/3
x = (1,65)1/3
x = 1,182 = coeficiente
x = (1,182 - 1) = (0,182 * 100) = 18,2% = porcentual
Observação: * = multiplicado = multiplicador
Veja as informações complementares, assim como Lista de Exercícios no BRASIL ESCOLA / UOL
NOTA BIBLIOGRÁFICA
PARADA FILHO, Américo Garcia. "ESTATÍSTICA - DESCRIÇÃO DE DADOS - MÉDIA GEOMÉTRICA". COSIF Eletrônico - Portal de Contabilidade. São Paulo, 18/08/2021. CURSOS. Disponível em https://www.cosif.com.br/publica.asp?arquivo=estatistica-0202. Acessado segunda-feira, 9 de março de 2026.

Megale Mídia Interativa Ltda. CNPJ 02.184.104/0001-29.
©1999-2026 Cosif-e Digital. Todos os direitos reservados.
